Grafisk løsning af ligninger
Ikke alle ligninger kan løses ved beregning, og derfor kan man have brug for andre metoder. Her vil vi se på, hvordan man kan finde løsninger til ligninger ved hjælp af grafer.
Lad os for eksemplets skyld se på en simpel lineær ligning: {$$x-1 = -x+5$$} De to udtryk, som står på henholdsvis venstre- og højresiden af lighedstegnet - altså {$x-2$} og {$-x+5$} - repræsenterer størrelser, hvis værdi afhænger af variablen x. Disse størrelser kunne vi kalde y, og vi får så udtrykkene: {$$y=x-1 \quad \text{og} \quad y=-x+5$$} Disse to ligninger kan afbildes i et koordinatsystem med x-værdierne ud ad den vandrette akse (x-aksen) og y-værdierne op ad den lodrette akse (y-aksen), som vist på figuren herunder. Der er tale om lineære funktioner, hvis grafer er rette linier.
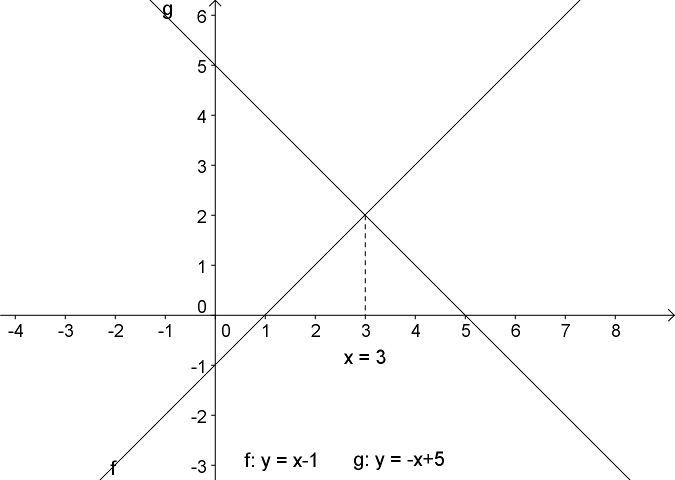
I denne applet kan du justere a og b værdierne for begge de to lineære funktioner og se hvordan grafernes skæringspunkt ændres
Det ses, at der er en enkelt x-værdi, hvor y-værdierne er ens for de to grafer, nemlig x-værdien for det punkt, hvor de skærer hinanden (x=3). For x-værdien x=3 har udtrykkene {$x-1$} og {$-x+5$} altså samme værdi - ligningen {$x-1 = -x+5$} er altså sand - og x=3 er derfor en løsning til ligningen (det kontrolleres let ved at indsætte x=3 i ligningen).
Lad os se på et andet eksempel:
{$$x^2 = x+2$$}
På figuren herunder ses graferne for funktionerne {$y = x^2$} og {$y = x+2$}.
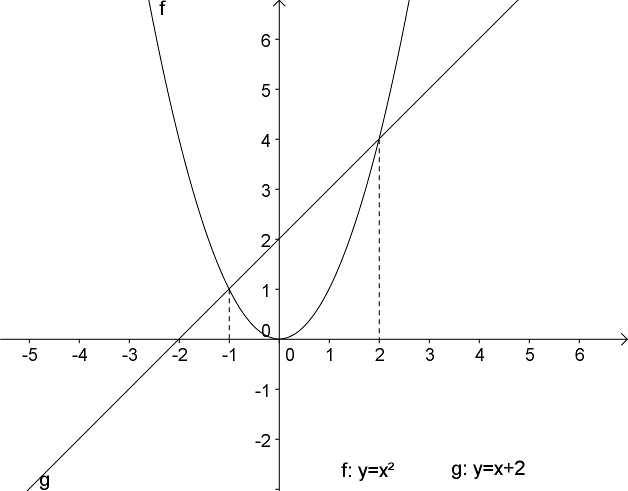
Her er der to skæringspunkter med x-koordinaterne x=-1 og x=2, som altså er løsninger til ligningen (tjek selv ved at indsætte dem). Der er to løsninger fordi ligningen jo er en andengradsligning.
Men hvad nu hvis vi omskriver ligningen til en af formerne: {$$x^2-x = 2 \quad \text{eller} \quad x^2-x-2=0$$} Da udtrykkene på de to sider af lighedstegnet herved ændres, skal der tegnes andre grafer, men som det fremgår af figurerne herunder, vil de nye grafers skæringspunkter stadig have x-koordinaterne x=-1 og x=2. Det er selvfølgelig ikke så overraskende, for de omskrevne ligninger har jo de samme løsninger som den oprindelige.
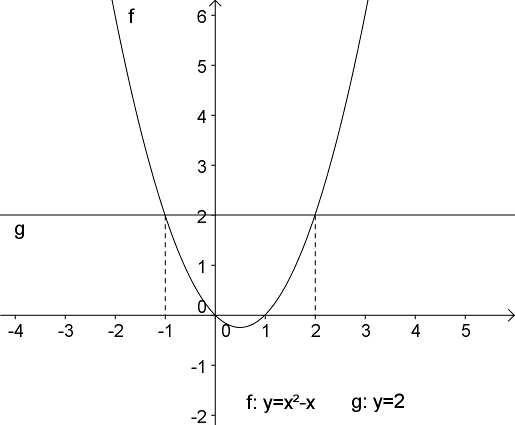 |
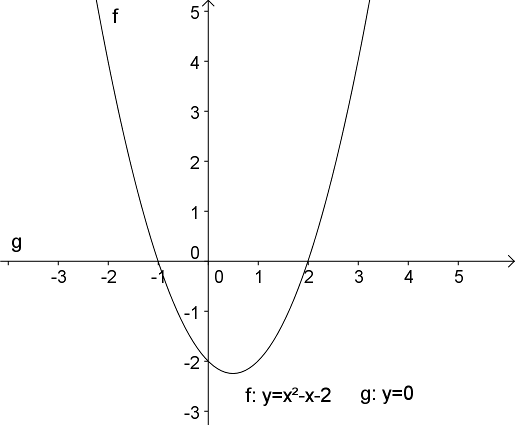 |
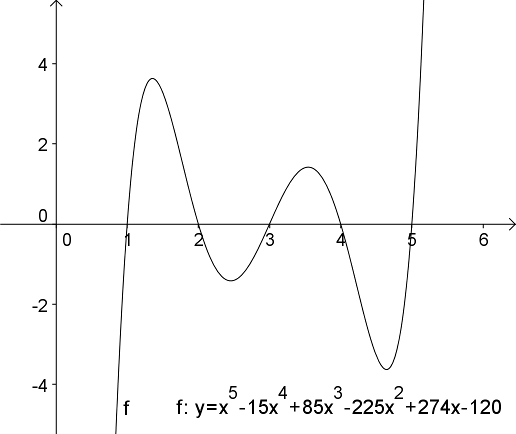
Lad os som et sidste eksempel se på en ligning, som ville være umulig at løse ved beregning:
{$$x^5-15x^4+85x^3-225x^2+274x-120=0$$}
Figuren herunder viser grafen for funktionen {$f(x)=x^5-15x^4+85x^3-225x^2+274x-120$}. Ligningens løsninger er x-koordinaterne for denne funktions skæringspunkter med x-aksen. Det ses, at der er fem løsninger: x=1, x=2, x=3, x=4 og x=5 (og da der er tale om et femtegradspolynomium, som jo højst har fem rødder, kan det udelukkes, at der kunne være flere løsninger udenfor det vindue, som grafen er vist i).