Lineære funktioner
Forskrift og graf
En lineær funktion er en funktion, hvis graf er en ret linje (heraf navnet). Lineære funktioner har en forskrift af formen {$$y=a \cdot x + b$$} eller da {$y=f(x)$} {$$f(x)=a \cdot x + b$$} hvor a og b er konstanter (som kan antage alle mulige værdier)

Konstanten a kaldes funktionens hældningskoefficient (eller stigningstal). Tallet angiver, hvor meget funktionens y-værdi vokser, når x-værdien øges med 1 (hvor meget vi skal gå op ad y-aksen, når vi går en ud ad x-aksen). Hvis a er et negativt tal bliver y-værdien mindre, når x-værdien øges.
a's betydning kan vises matematisk på følgende måde
Vi ser på, hvad funktionsværdien bliver, hvis vi lægger 1 til x-værdien (vi indsætter x+1 på x's plads i forskriften) {$$ f(x+1)=a \cdot (x+1)+b$$} Vi ganger så parentesen på højresiden ud {$$ f(x+1)=a \cdot x +a+b$$} og flytter lidt rundt {$$ f(x+1)=a \cdot x +b+a$$} Endelig udnytter vi, at {$a \cdot x+b = f(x) $} {$$ f(x+1)=f(x)+a$$} Heraf ses, at funktionsværdien (y-værdien) i x+1 fås ved at lægge a til funktionsværdien i x. Altså vokser funktionsværdien med a, når x-værdien vokser med 1
Konstanten b er funktionsværdien når x=0 (altså den værdi, hvor funktionens graf skærer y-aksen) Det ses af følgende udregning
{$$f(0)=a \cdot 0 + b = b$$}
Appletten herunder viser grafen for en lineær funktion. Læg mærke til den lille trekant, som viser, hvor meget y-værdien øges (eller aftager) med, når x-værdien øges med 1. Du kan undersøge betydningen af a og b's værdier ved at indstille skyderne øverst til venstre

Klik for at starte appletten
Bestemmelse af forskriften
Hvis vi kender to punkter, kan vi finde forskriften (altså a og b) for den lineære funktion, hvis graf går gennem disse to punkter, på følgende måde:
|
Lad der være givet to punkter {$(x_1, y_1)$} og {$(x_2, y_2)$} Først findes a ved hjælp af formlen {$$a= \frac{y_2-y_1}{x_2-x_1}$$} Dernæst findes b ved en af formlerne (de giver samme resultat, så der er frit valg) {$$b=y_1-ax_1 \quad eller \quad b = y_2-ax_2$$} |
Bevis
Formlen for a
Først indsættes de to punkter i forskriften {$$y_1=ax_1+b \quad og \quad y_2=ax_2+b$$} Vi trækker så den første ligning fra den sidste {$$y_2-y_1 = ax_2+b-(ax_1+b)$$} Minusparentesen hæves {$$y_2-y_1 = ax_2+b-ax_1-b$$} b'erne går ud med hinanden {$$y_2-y_1 = ax_2-ax_1$$} a sættes uden for parentes {$$y_2-y_1 = a(x_2-x_1)$$} Endelig divideres der over {$$\frac{y_2-y_1}{x_2-x_1}=a$$} Eller som vi plejer at skrive det {$$a=\frac{y_2-y_1}{x_2-x_1}$$}
Formlen for b
Her indsættes punkterne igen i forskriften (her kun vist for det første punkt) {$$y_1=ax_1+b$$} Og b isoleres {$$y_1-ax_1=b$$} Eller {$$b=y_1-ax_1$$}
Eksempel
Opgave: Bestem forskriften for den lineære funktion der går gennem punkterne (2,0) og (6,2)
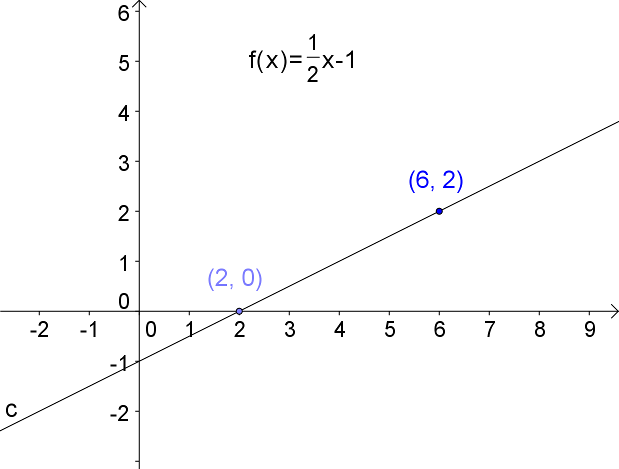
Løsning: vi sætter {$x_1=2, y_1=0, x_2=6 \quad og \quad y_2=2$} og indsætter i formlen for a {$$a=\frac{y_2-y_1}{x_2-x_1}$$} {$$a=\frac{2-0}{6-2}$$} {$$a=\frac{1}{2}$$} Dernæst finder vi b ved at indsætte i formlen {$$b=y_1-ax_1$$} {$$b=0-\frac{1}{2} \cdot 2$$} {$$b=-1$$} Og forskriften bliver så {$$f(x)=\frac{1}{2}x-1$$}
Funktionens graf ses herunder
Den lineære vækstform
Lineære funktioner vokser (ikke overraskende) lineært, d.v.s. at en bestemt absolut tilvækst i x-værdien giver en bestemt (anden) absolut tilvækst i y-værdien, lige meget hvor vi starter. Vi kan vise dette matematisk og udregne hvor stor y's tilvækst bliver på følgende måde
Vi kalder tilvæksten i x-værdien {$\Delta x$}. Vi siger, at vi starter i punktet (x,f(x)), og så øger vi x-værdien med {$\Delta x$} og undersøger, hvad der sker med y-værdien (f(x)-værdien). Vi skal altså se på {$f(x+\Delta x)$}
{$$f(x+\Delta x) = a \cdot (x+\Delta x) + b$$} Vi ganger så parentesen på højresiden ud {$$ f(x+\Delta x)=a \cdot x +a \cdot \Delta x+b$$} og flytter lidt rundt {$$ f(x+\Delta x)=a \cdot x +b+a\cdot \Delta x$$} og endelig {$$ f(x+\Delta x)=f(x)+a \cdot \Delta x$$}
Vi ser altså, at når x-værdien øges med den absolutte værdi {$\Delta x$}, så øges y-værdien med {$a \cdot \Delta x$}
Eksempel: En lineær funktion har forskriften {$f(x)=2 \cdot x-3$}. Hvis vi fx øger x-værdien med 5 ({$\Delta x=5$}), vil y-værdien altså øges med {$2 \cdot 5=10$} (ligegyldigt hvilken x-værdi, vi starter fra)