Andengradsligninger
Andengradsligninger er ligninger, hvor den variable (ofte x) optræder i (højst) anden potens. De har følgende generelle form
{$$ a\cdot x^2 + b\cdot x+c=0 $$}
hvor a, b og c er konstanter, som kan have vilkårlige værdier (bortset fra at a ikke må være nul, da der jo så ikke er tale om en andengradsligning). Konstanterne a og b kaldes også koefficienter: a er koefficienten til {$x^2$} og b er koefficienten til x.
Fremgangsmåden ved løsningen af en andengradsligning er som følger:
|
Andengradsligningen {$$ a\cdot x^2 + b\cdot x+c=0 $$} løses på følgende måde: Først beregnes den såkaldte diskriminant {$d=b^2-4ac$} Diskriminantens fortegn "bestemmer", hvor mange løsninger der er (0, 1 eller 2). Antallet af løsninger og formler til at beregne løsningerne er: For d<0 er der ingen løsninger For d=0 er der en løsning, som findes v.h.a. formlen {$$ \displaystyle x=-\frac{b}{2a}$$} For d>0 er der to løsninger, som findes v.h.a. formlen {$$ \displaystyle x=\frac{-b\pm \sqrt{d} }{2a} $$} NB! {$\pm$} i den sidste formel betyder, at den ene af de to løsninger beregnes ved at bruge minusset og den anden ved at bruge plusset |
Eksempler
Eksempel 1: Løs ligningen {$3x^2-3x-6=0$}
Løsning:
Først identificeres konstanterne a, b og c {$$a=3 \quad b=-3 \quad c=-6$$} Derefter beregnes d {$$d=b^2-4ac=(-3)^2-4\cdot3\cdot(-6)=81$$} Da d>0 er der to løsninger, som findes ved hjælp af formlen {$$ x=\frac{-b\pm \sqrt{d} }{2a} $$} {$$ x=\frac{-(-3)\pm \sqrt{81}}{2\cdot3} $$} De to løsninger er dermed {$$x_1=-1 \quad \vee \quad x_2=2$$}
Eksempel 2: Løs ligningen {$2x^2-8x+8=0$}
Løsning:
a, b og c identificeres {$$a=2 \quad b=-8 \quad c=8$$} Diskriminanten udregnes {$$d=b^2-4ac=(-8)^2-4\cdot2\cdot8=0$$} Da d=0 er der kun en løsning, som beregnes ved hjælp af formlen {$$ x=-\frac{b}{2a}$$} {$$ x=-\frac{-8}{2\cdot2}$$} {$$ x=2 $$}
Eksempel 3: Løs ligningen {$x^2+2x+3=0$}
Løsning:
a, b og c identificeres {$$a=1 \quad b=2 \quad c=3$$} Diskriminanten udregnes {$$d=b^2-4ac=(2)^2-4\cdot1\cdot3=-8$$} Da d<0 er der ingen løsninger
Eksempel 4: Løs ligningen {$x^2=-x+2$}
Løsning:
Her skal ligningen først omskrives til standardformen (hvor der står nul på højresiden) {$$x^2=-x+2$$} {$$x^2+x-2=0$$} Så kan a, b og c identificeres {$$a=1 \quad b=1 \quad c=-2$$} Diskriminanten udregnes {$$d=b^2-4ac=(1)^2-4\cdot1\cdot(-2)=9$$} Da d>0 er der to løsninger, som beregnes {$$ x=\frac{-1\pm \sqrt{9}}{2\cdot1} $$} De to løsninger er altså {$$x_1=-2 \quad \vee \quad x_2=1$$}
NB! I tilfælde hvor c=0 er det smartest at bruge Nulreglen
Eksempel
Løs ligningen {$x^2-2x=0$}
Løsning: {$$x^2-2x=0$$} x sættes udenfor parentes {$$x(x-2)=0$$} Nulreglen giver så {$$x=0 \quad \vee \quad x-2=0$$} {$$x=0 \quad \vee \quad x=2$$}
Grafisk løsning af andengradsligninger
Venstresiden i en andengradsligning er et såkaldt andengradspolynomium. Det er en funktion med forskriften
{$$ f(x)=a\cdot x^2 + b\cdot x+c $$}
At løse andengradsligningen svarer således til at finde x-værdier, hvor f(x)=0, d.v.s. x-værdier hvor funktionens graf skærer x-aksen.
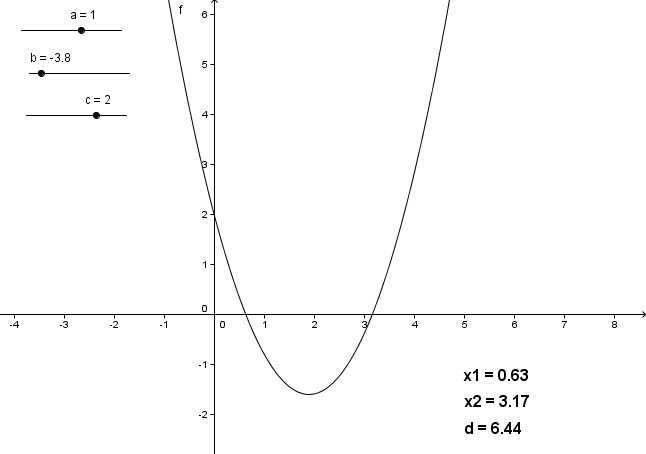
Dette er illustreret i nedenstående applet. Den viste parabel er grafen for andengradspolynomiet {$f(x)=ax^2+bx+c$} med de viste værdier af a, b og c. De viste værdier for x1 og x2 er løsningerne til ligningen {$f(x)=ax^2+bx+c=0$} udregnet ved hjælp af formlerne ovenfor. Prøv at ændre værdierne af a, b og c ved hjælp af "skyderne" og læg mærke til, at x1 og x2 hele tiden er x-værdierne for parablens skæringspunkter med x-aksen. Diskriminanten d er også vist - læg mærke til, at parablen ikke krydser x-aksen, når d<0, netop rører den i et enkelt punkt, når d=0 og skærer den i to punkter, når d>0
Klik for at starte appletten