Bevis for (1)

Vi bruger tretrinsreglen til at finde differentialkvotienten for f(x)=sin(x):

Trin 1: {$$\Delta f = sin(x_0+h)-sin(x_0)$$} Vi bruger nu følgende logaritmiske formel: {$\displaystyle sin(u)-sin(v) = 2 \cdot cos(\frac{u+v}{2}) \cdot sin(\frac{u-v}{2})$} til at omskrive udtrykket

{$$\Delta f = 2 \cdot cos(\frac{x_0+h+x_0}{2}) \cdot sin(\frac{x_0+h-x_0}{2})$$} {$$\Delta f = 2 \cdot cos(\frac{2x_0+h}{2}) \cdot sin(\frac{h}{2})$$} {$$\Delta f = 2 \cdot cos(x_0+\frac{h}{2}) \cdot sin(\frac{h}{2})$$} Trin 2: {$$\frac{\Delta f}{h} = \frac{2 \cdot cos(x_0+\frac{h}{2}) \cdot sin(\frac{h}{2})}{h}$$} {$$\frac{\Delta f}{h} = \frac{cos(x_0+\frac{h}{2}) \cdot sin(\frac{h}{2})}{\frac{h}{2}}$$} {$$\frac{\Delta f}{h} = cos(x_0+\frac{h}{2}) \cdot \frac{sin(\frac{h}{2})}{\frac{h}{2}}$$} Vi lader nu h og dermed {$\frac{h}{2}$} gå mod 0

Da cos er en kontinuert funktion gælder {$cos(x_0+\frac{h}{2}) \rightarrow cos(x_0) \quad for \quad h \rightarrow 0$}

Vi vender nu opmærksomheden mod brøken {$\displaystyle \frac{sin(\frac{h}{2})}{\frac{h}{2}}$}, som er mere tricky:

Vi kalder midlertidigt brøken {$\displaystyle \frac{sin(x)}{x}$} og betragter figuren herunder.

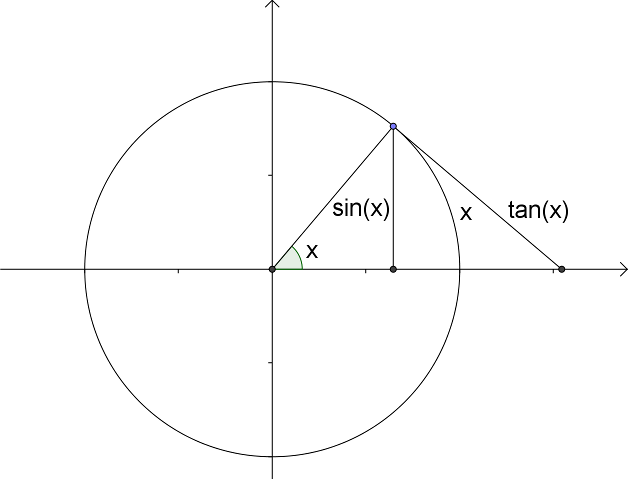
Det fremgår, at sin(x) må være mindre end x, som igen er mindre end tan(x) eller med matematisk notation {$$sin(x) \leq x \leq tan(x)$$}

Vi kan nøjes med at se på positive x-værdier, da {$\displaystyle \frac{sin(x)}{x} = \frac{sin(-x)}{-x}$} (følger af at {$sin(-x) = -sin(x)$}). Vi kan derfor dividere uligheden med x og får så {$$\frac{sin(x)}{x} \leq 1 \leq \frac{tan(x)}{x}$$} Vi deler uligheden op i to {$$\frac{sin(x)}{x} \leq 1 \qquad og \qquad 1 \leq \frac{tan(x)}{x}$$} Den højre ulighed omskrives {$$\frac{sin(x)}{x} \leq 1 \qquad og \qquad 1 \leq \frac{sin(x)}{cos(x) \cdot x}$$} For {$x < \frac{\Pi}{2}$} er {$cos(x) > 0$} og vi kan derfor gange med {$cos(x)$} {$$\frac{sin(x)}{x} \leq 1 \qquad og \qquad cos(x) \leq \frac{sin(x)}{x}$$} Vi kan nu samle de to uligheder på følgende måde {$$cos(x) \leq \frac{sin(x)}{x} \leq 1$$} Da {$cos(x) \rightarrow 1 \quad for \quad x \rightarrow 0 \ $} og {$\displaystyle \frac{sin(x)}{x}$} er "klemt inde" mellem cos(x) og 1 må der også gælde, at {$\displaystyle \frac{sin(x)}{x} \rightarrow 1 \quad for \quad x \rightarrow 0$}

Trin 3

Vi vender nu tilbage til udtrykket {$$\frac{\Delta f}{h} = cos(x_0+\frac{h}{2}) \cdot \frac{sin(\frac{h}{2})}{\frac{h}{2}}$$} Da brøken {$\displaystyle \frac{sin(\frac{h}{2})}{\frac{h}{2}}$} går mod 1 for h gående mod 0 må der gælde {$$\frac{\Delta f}{h} = cos(x_0+\frac{h}{2}) \cdot \frac{sin(\frac{h}{2})}{\frac{h}{2}} \rightarrow cos(x_0) \quad for \quad h \rightarrow 0 $$} eller altså {$$sin'(x_0) = cos(x_0)$$} eller da ovenstående kan udføres for alle værdier af {$x_0$} {$$sin'(x) = cos(x)$$} Som var det, vi skulle vise.

Bevis for (3)

(3) vises lettest ved at bruge (1) og (2) samt formlen for differentiation af en brøk. {$$tan(x) = \frac{sin(x)}{cos(x)}$$} {$$tan'(x) = \Big(\frac{sin(x)}{cos(x)} \Big)'$$} {$$tan'(x) = \frac{sin'(x)cos(x) - sin(x)cos'(x)}{(cos(x))^2}$$} {$$tan'(x) = \frac{cos(x)cos(x) - sin(x)(-sin(x))}{(cos(x))^2}$$} {$$tan'(x) = \frac{(cos(x))^2 + (sin(x))^2}{(cos(x))^2}$$} {$$tan'(x) = \frac{1}{(cos(x))^2}$$} Som let ses at være lig med {$1+(tan(x))^2$}