Mængder
En mængde er en slags "beholder", som kan indeholde en samling af såkaldte elementer. Elementerne kan i princippet være alle mulige objekter, men her vil vi kun se på mængder, som indeholder tal.
En mængde, som indeholder et endeligt antal elementer, kaldes en endelig mængde, og en mængde, som indeholder uendeligt mange elementer, kaldes en uendelig mængde. Et eksempel på en endelig mængde er mængden, der indeholder tallene 1, 2, 3, 4 og 5. Eksempler på uendelige mængder er mængden af positive hele tal (N) og mængden af alle (reelle) tal mellem fx 0 og 1.
Mængder navngives med store bogstaver, fx A, B osv.
Mængder kan skrives på forskellige måder afhængigt af hvilken type mængde, der er tale om.
Listeform
Nogle mængder kan skrives på listeform, hvor elementerne blot opremses. Her er nogle eksempler:
|
{$A=\{ 1,2,3,4,5 \}$} |
Mængden som indeholder tallene 1, 2, 3, 4 og 5 |
|
{$A=\{ 1,2,3, \dots ,100 \}$} |
Mængden som indeholder de hele tal fra 1 til 100. De tre prikker betyder "fortsæt på samme måde", d.v.s. efter det "mønster" som er angivet af tallene før prikkerne. Her er mønsteret selvfølgelig, at der hele tiden skal lægges en til den foregående værdi, og derfor fortsætter sekvensen med 4, 5, 6 o.s.v. hele vejen op til 100 |
|
{$A=\{ 1,2,3, \dots \}$} |
Mængden som indeholder alle positive hele tal. Her er der ikke noget tal efter prikkerne, og sekvensen fortsætter derfor mod uendelig (der er altså tale om en uendelig mængde). |
|
{$A=\{ -100,-99,-98, \dots ,99, 100\}$} |
Mængden som indeholder alle hele tal fra -100 til 100 |
Mængdebyggeren
Mængder kan også skrives ved hjælp af den såkaldte mængdebygger. Her er et eksempel:
|
{$A=\{ n \in N \ \vert \ 1\leq n \leq 5\}$} |
Mængden som indeholder tallene 1, 2, 3, 4 og 5, altså mængden som også kan skrives {$A=\{ 1,2,3,4,5 \}$}. |
Læg mærke til, at området mellem de to krøllede parenteser er opdelt i to ved hjælp af den lodrette streg. På venstresiden af denne angives hvilken type elementer, der er tale om, ved at skrive hvilken "grundmængde" elementerne tilhører. I dette tilfælde står der, at elementerne, som her angives som {$n$}, tilhører (symbolet {$\in$}) mængden af naturlige tal N (positive, hele tal - se Talmængder). Efter den lodrette streg angives hvilken del af grundmængdens elementer, som mængden indeholder. Her står der, at elementerne er mindre end eller lig med 5 og større end eller lig med 1. Altså indeholder mængden tallene 1, 2, 3, 4 og 5. Læg mærke til at det egentlig ikke er nødvendigt at skrive {$ 1\leq n $}, da det jo følger af at {$n \in N$}
Her er nogle flere eksempler:
|
{$A=\{ n \in N \ \vert \ n\leq 100\}$} |
Mængden som indeholder de hele tal fra 1 til 100. |
|
{$A=\{ n \in Z \ \vert \ -100\leq n \leq 100 \}$} |
Mængden som indeholder de hele tal mellem -100 og 100. |
|
{$A=\{ x \in R \ \vert \ -1\leq x \leq 1 \}$} |
Mængden som indeholder alle REELLE tal - altså ALLE tal - mellem -1 og 1. Der er tale om en uendelig mængde. |
Intervaller
Et interval er en mængde, som indeholder alle reelle tal mellem to værdier. Det sidste eksempel ovenfor er således et interval. Som regel skrives intervaller dog med en særlig intervalnotation, som der her kommer en række eksempler på:
|
{$\left[-1;1 \right]$} |
Intervallet (mængden) som indeholder alle reelle tal mellem -1 og 1. Læg mærke til at der bruges firkantparenteser, og at de to talværdier adskilles af et semikolon (;). Når firkantparenteserne vender som her, altså så de små streger vender ind mod tallene, betyder det, at de to tal -1 og 1 er inkluderet i intervallet. Et sådant interval, hvor endepunkterne er inkluderet, kaldes i øvrigt et lukket interval. |
|
{$\left]-1;1 \right[$} |
Intervallet som indeholder alle reelle tal mellem -1 og 1 som ovenfor, bortset fra at endepunkterne -1 og 1 ikke er med i intervallet. Et sådant interval, hvor endepunkterne ikke er inkluderet, kaldes et åbent interval. |
|
{$\left]0;100 \right]$} |
Intervallet som indeholder alle reelle tal mellem 0 og 100, hvor 0 ikke er med, mens 100 er med. Et sådant interval kaldes et halvåbent interval. |
|
{$\left]0;\infty \right[$} |
Intervallet bestående af alle positive reelle tal. Tegnet {$\infty$} betyder "uendelig" og det regnes ikke for et egentligt tal. Intervallet skal derfor altid være åbent, hvis "endepunktet" er {$\infty$}. |
|
{$\left]-\infty ;0 \right]$} |
Intervallet bestående af alle negative reelle tal samt tallet 0. |
Intervaller kan illustreres ved at afbilde dem på en tallinie. Nogle eksempler ses på figuren herunder. Læg mærke til, at intervallets udstrækning vises med en vandret linie. Intervalendepunkter vises med en "bolle", som enten kan være udfyldt - i så fald er det tal, som bollen er placeret ved med i mængden - eller ikke udfyldt (tom) - så er tallet selvfølgelig ikke med i mængden. Hvis linien ikke afsluttes med en bolle, antages den at gå til {$\infty$} eller {$-\infty$}
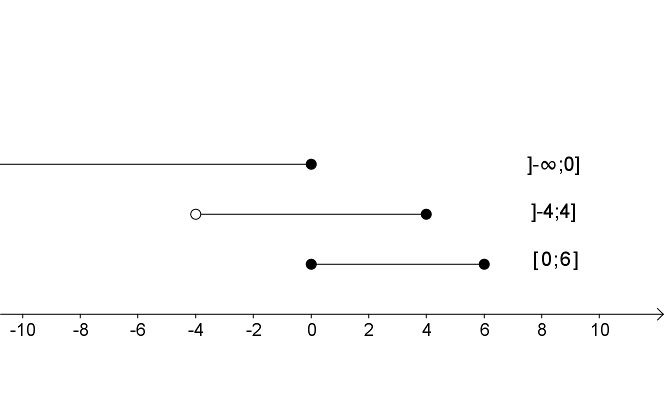
Klik for at starte appletten
Nogle særlige mængder
Den tomme mængde, altså den mængde som ikke indeholder nogen elementer, betegnes Ø
Ved løsning af ligninger, taler man ofte om løsningsmængden, som betegnes L. Hvis en ligning ikke har nogen løsninger, skriver man L=Ø.
Tallene underinddeles i en række mængder - se Talmængder
Mængdeoperationer
Fællesmængden mellem to mængder består af de elementer, som tilhører begge mængder. Fællesmængden mellem mængderne A og B skrives {$A \cap B$}
Foreningsmængden mellem to mængder består af de elementer, som tilhører mindst en af mængderne. Foreningsmængden mellem mængderne A og B skrives {$A \cup B$}
Differensmængden mellem to mængder består af de elementer, som tilhører den første mængde men ikke den anden. Differensmængden mellem A og B, som skrives {$A \setminus B$} består altså af elementer, som tilhører A men ikke B.
Eksempler: Hvis {$A = \{ 1,2,3,4,5 \}$} og {$B = \{ 4,5,6,7,8 \}$} gælder følgende:
|
{$A \cap B = \{ 1,2,3,4,5 \} \cap \{ 4,5,6,7,8 \} = \{ 4,5 \}$} {$A \cup B = \{ 1,2,3,4,5 \} \cup \{ 4,5,6,7,8 \} = \{ 1,2,3,4,5,6,7,8 \}$} {$A \setminus B = \{ 1,2,3,4,5 \} \setminus \{ 4,5,6,7,8 \} = \{ 1,2,3 \}$} |
Mængdeoperationerne er også illustreret v.h.a. såkaldte Venn diagrammer nederst på siden.
Relationer mellem mængder
To mængder A og B er lig med hinanden, hvis de indeholder de samme elementer. Vi skriver i så fald A=B
En mængde A er en delmængde af mængden B, hvis alle elementer i A også er elementer i B. Vi skriver {$A \subseteq B$}
To mængder, som ikke har nogen fælles elementer, kaldes disjunkte mængder. Hvis A og B er disjunkte mængder gælder altså {$A \cap B = Ø $}
Venn diagrammer
Mængder og mængdeoperationer illustreres ofte ved hjælp af såkaldte Venn diagrammer:

De to cirkler repræsenterer de to mængder A og B. Cirklerne overlapper, fordi mængderne A og B har fælles elementer. Fællesmængden {$A \cap B$} er således det grønne område. Foreningsmængden {$A \cup B$} er hele området indenfor de to cirkler, altså det røde, det grønne og det gule område tilsammen. Differensmængden {$A \setminus B$} er det røde område, mens differensmængden {$B \setminus A$} er det gule område.