Grundlæggende færdigheder

Led

Hvis man vil lære matematik er det nødvendigt at sætte sig ind i det matematiske sprog, så man kan læse matematiske tekster og forstå, hvad læreren siger. Desuden er det selvfølgelig vigtigt, at man selv lærer at bruge det matematiske sprog korrekt, hvis man ønsker at kommunikere med andre om matematik - fx lærer og censor ved eksamen.

Det matematiske sprog er ekstremt kompakt og præcist, og er derfor et effektivt redskab til at udtrykke talmæssige sammenhænge, men det virker selvfølgelig kun, hvis man har helt styr på de forskellige termer, symboler og begreber og forstår at bruge dem korrekt. Her på siden står der lidt om en række helt grundlæggende ting, som man bør kunne.

Variable og konstanter

En variabel er et symbol, som "står for" en talværdi. Eller rettere sagt for forskellige talværdier, for det hedder selvfølgelig en variabel, fordi dens værdi kan variere. De symboler, der bruges, er som regel små bogstaver fra den sidste del af alfabetet. De mest almindelige er x og y, men også t ses ofte (især når den variable størrelse er tiden). Når den variable kun kan antage heltalsværdier bruges ofte n.

En konstant er også et symbol, som "står for" en talværdi, men her ligger værdien selvfølgelig fast (den er konstant). Der anvendes som regel små bogstaver fra den første del af alfabetet. De mest almindelige er a, b og c, men også k (for konstant) ses ofte. Sommetider ønsker man at tale om en bestemt fast værdi, som en variabel kan antage. Hvis den variable hedder x, kan en sådan konstant x-værdi angives ved et x med et passende indeks (skrevet med sænket skrift) som for eksempel {$x_0$}, {$x_1$} eller {$x_2$} (udtales "x nul", "x et" og "x to"). Hvis den variable hedder y skriver man selvfølgelig tilsvarende {$y_0$}, {$y_1$} eller {$y_2$} ("y nul", "y et", "y to").

NB! Det er meget vigtigt at kende forskel på {$x_2$} og {$x^2$} (og at sige dem rigtigt: henholdsvis "x to" og "x i anden"). {$x_2$} angiver som nævnt en fast, konstant x-værdi, mens {$x^2$} betyder {$x \cdot x$}, som jo ikke er en konstant (værdien afhænger af værdien af x).

Led

Led er udtryk som lægges sammen eller trækkes fra hinanden. I følgende udtryk {$$2+5-8+3$$} er der således fire led, nemlig de fire tal.

I udtrykket {$$3 \cdot x^2 - 4 \cdot x+1$$} er der tre led, nemlig udtrykkene {$3 \cdot x^2$}, {$4 \cdot x$} og {$1$}

Faktorer

Faktorer er udtryk som ganges med hinanden. I følgende udtryk {$$a \cdot b \cdot c$$} er der tre faktorer, nemlig a, b og c

I udtrykket {$$3 \cdot \frac{2}{7} \cdot (x+1)$$} er der også tre faktorer, nemlig 3, {$\displaystyle \frac{2}{7}$} og (x+1)

Matematiske udtryk består, som det også fremgår af ovenstående eksempler, ofte af både led og faktorer. Her er et andet eksempel: {$$3 \cdot \frac{x^2-4}{3 \cdot x} + \sqrt{2} \cdot (x-5)$$} Her er der overordnet to led, som hver især består af blandinger af faktorer og led.

Leds og faktorers orden (rækkefølge)

Ved addition (+) er leddenes orden ligegyldig. Altså gælder der: {$$a+b = b+a$$} Ved subtraktion (-) er leddenes orden ikke ligegyldig, {$$a-b \ne b-a$$} {$\ne$} (et overstreget lighedstegn) betyder selvfølgelig "ikke lig med".
Subtraktion kan dog opfattes som addition af et negativt tal {$$a-b = a+(-b)$$} Og derfor bliver leddenes orden ligegyldig, hvis blot minusset følger med det tal, det står foran. Der gælder altså {$$a-b = a+(-b) = -b+a$$} Ved multiplikation er faktorernes orden ligegyldig {$$a \cdot b = b \cdot a$$} Ved division kan man ikke bare bytte om på tæller og nævner {$$\frac{a}{b} \ne \frac{b}{a}$$}

Skjulte tegn

Positive tal skrives blot som tallet selv uden fortegn. Skriver vi fx 7, mener vi det positive tal 7, så der står egentlig et skjult + foran syvtallet.

Negative tal skrives derimod med fortegn, fx -7

I såkaldte blandede tal, som består af en helt tal og en brøk, der faktisk skal lægges sammen, udelades plusset. Fx betyder {$2 \frac{1}{2}$} jo egentlig {$2 + \frac{1}{2}$}

Når et tal ganges med en variabel (fx x) eller en parentes udelades gangetegnet. Her er nogle eksempler: {$$2x = 2 \cdot x \qquad 2(x-1) = 2 \cdot (x-1)$$}

Tallet, der står foran en variabel, kaldes i øvrigt en koefficient

Lighedstegnet

Lighedstegnet betyder - ikke overraskende - at de to udtryk, der står på de to sider af lighedstegner er lig med hinanden (altså at de har samme værdi). Det gælder ALTID, og det er FORBUDT at skrive et lighedstegn, hvis det, der står på de to sider, ikke har samme værdi. En almindelig fejl er "at regne videre" på et resultat som i følgende udregning:

{$$2 \cdot 5 = 10 + 2 = 12 - 7 = 5$$}

Det er selvfølgelig rigtigt, at {$2 \cdot 5 = 10$}, men det er ikke rigtigt, at {$2 \cdot 5 = 10 + 2$}. Her giver udtrykket på venstresiden jo 10, mens udtrykket på højresiden giver 12, og 10 og 12 er ikke lig med hinanden. Regnestykket burde i stedet skrives: {$$2 \cdot 5 + 2 - 7 = 5$$}

Betydende cifre og afrunding

Når man foretager en udregning - fx på sin lommeregner - får man ofte resultatet i form af et kommatal med masser af cifre (antallet afhænger af lommeregnerens interne repræsentation af de tal, den arbejder med). Som regel er det dog ikke hensigtsmæssigt at angive resultatet med så mange cifre. I nogle tilfælde er der ikke brug for at angive resultatet med stor nøjagtighed, og i andre tilfælde er det decideret forkert, fordi de tal, man har brugt til at udregne resultatet, ikke har været tilsvarende nøjagtige.

Når man skal angive et tal med et bestemt antal cifre, sker det som regel ved at "afrunde" tallet. Det foregår på den måde, at det første ciffer efter det sidste ciffer, man ønsker at angive, bestemmer om der skal rundes op eller ned. Hvis dette ciffer er 5 eller derover, rundes der op, og hvis det er mindre end 5, rundes der ned. Hvis man fx vil afrunde tallet 1,2345 til 3 cifre, er det altså det fjerde ciffer, der afgør, om der skal rundes op eller ned. I dette tilfælde er det fjerde ciffer 4, og da det er mindre end 5 skal der rundes ned. og det afrundede tal bliver derfor 1,23. Hvis tallet 1,2354 skal afrundes til tre cifre, bliver resultatet 1,24, fordi det fjerde ciffer er 5, og der derfor skal rundes op.

Antallet af cifre, som et tal er angivet med, fortæller, hvor præcist tallet er bestemt. Et tal som fx 1,23 skal nemlig - hvis ikke man får andet at vide - opfattes, som om det er afrundet og altså kan repræsentere et hvilket som helst tal i intervallet fra 1,225000... til 1,234999... (alle tal i dette interval vil jo give 1,23, hvis de afrundes til tre cifre). Tallet 1,2345 repræsenterer på samme måde alle tal i intervallet fra 1,23445000... til 1,23454999..., som jo er et snævrere interval, og tallet er derfor selvfølgelig mere præcist bestemt.

Det betyder også, at der eksempelvis er forskel på at skrive 1,2 og 1,200. Det sidste tal er mere præcist, fordi intervallet med tal, der giver 1,200 ved afrunding, er meget snævrere end intervallet, der giver 1,2 ved afrunding. Læg mærke til, at tal, som man ved er heltal, har uendelig mange betydende cifre. Der gælder således {$3 = 3,000...$}.

Antallet af cifre, som bestemmer hvilken præcision et tal er angivet med, kaldes ofte for antallet af betydende cifre. Tallet 1,2345 har fem betydende cifre mens 1,23 har tre betydende cifre. Tallet 1,200 har fire betydende cifre mens 1,2 har to betydende cifre. Når der er foranstillede nuller, tælles disse ikke med. Tallet 0,00012 har således kun to betydende cifre, mens 0,0001200 har fire betydende cifre. Læg i øvrigt mærke til, at tal, som man ved er heltal, har uendelig mange betydende cifre. Der gælder således {$3 = 3,000...$}.

Generelt bør resultater ikke opgives med flere betydende cifre end det tal i udregningen, som har det mindste antal betydende cifre. For eksempel bør resultatet af regnestykket {$3,1 \cdot 2,436$} angives med to betydende cifre, altså {$3,1 \cdot 2,436 = 7,6$}

Ved komplicerede regnestykker, hvor der laves mellemregninger, må mellemresultaterne ikke afrundes - der regnes videre med alle de cifre, lommeregneren kan klare. Først til sidst når det endelige facit skal angives, foretages en passende afrunding.

Koordinatsystemer og punkter

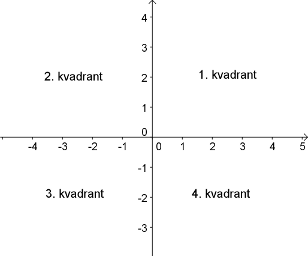
Et (kartesisk) koordinatsystem består af talakser, som står vinkelret på hinanden. På C-niveau arbejder vi kun med koordinatsystemer, som har to akser, en vandret og en lodret. Den vandrette akse kaldes også førsteaksen eller x-aksen, og den lodrette kaldes andenaksen eller y-aksen. Koordinatsystemet bruges til at fastlægge positionen af punkter i den plan, som de to akser ligger i. De to akser inddeler planen i fire område, som kaldes kvadranter. Disse nummereres som vist på figuren.

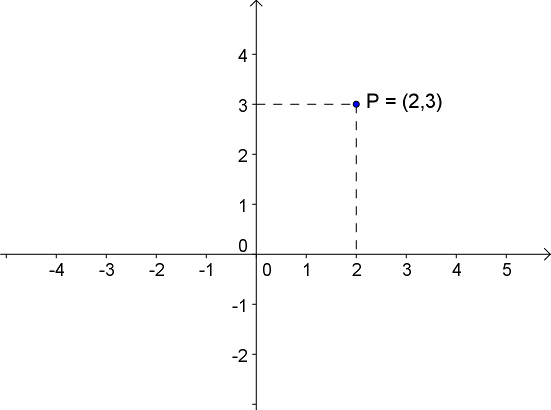
Et punkt består af to tal - punktets koordinater. De to tal skrives i en parentes og med komma imellem, fx {$P=(2,3)$}. Det første tal er x-koordinaten og det andet er y-koordinaten - HUSK DET NU!!! I eksemplet er x-koordinaten altså 2 og y-koordinaten 3. Punktets position i koordinatsystemet er skæringspunktet mellem den lodrette streg, som krydser x-aksen ved punktets x-koordinat og den vandrette streg, som krydser y-aksen ved punktets y-koordinat. Princippet er illustreret i appletten herunder.