Logaritmer

Logaritmefunktioner er omvendte funktioner til eksponentialfunktioner. Titalslogaritmefunktionen log(x) er således den omvendte funktion til eksponentialfunktionen 10^x. En anden logaritmefunktion, man ofte støder på, er den såkaldte naturlige logaritmefunktion ln(x), som er den omvendte funktion til den naturlige eksponentialfunktion e^x. Denne sammenhæng skrives matematisk på følgende måde:

{$$log(10^x)=x\quad og \quad 10^{log(x)}=x$$}

{$$ln(e^x)=x\quad og \quad e^{ln(x)}=x$$}

Logaritmefunktionernes grafer

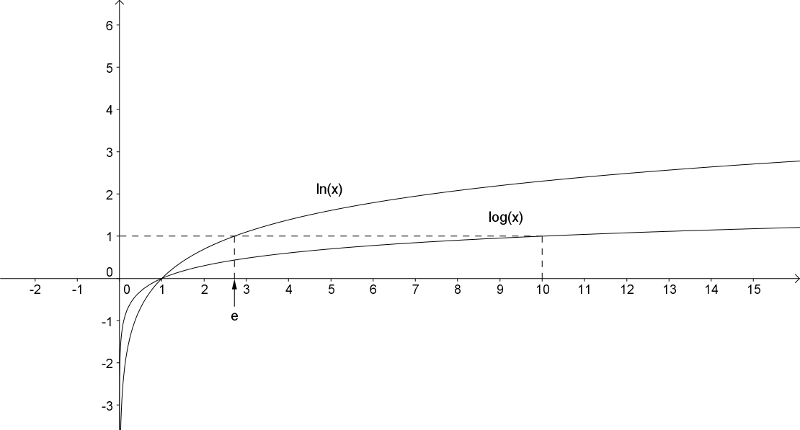
På figuren herunder ses den naturlige logaritmefunktion (ln) og titalslogaritmefunktionen (log). Læg mærke til, at x-værdien, som svarer til y-værdien 1, er e for den naturlige logaritme og 10 for titalslogaritmen. Læg også mærke til, at begge logaritmefunktioner går gennem punktet (1,0). Det ses også, at definitionsmængden for logaritmefunktionerne er alle positive tal, altså Dm=R₊, mens værdimængden er alle reelle tal, altså Vm=R. Logaritmefunktionerne er voksende i hele deres definitionsmængde, hvilket betyder, at der til hver y-værdi kun hører en x-værdi. På matematiksprog gælder der altså {$x_1 = x_2 \Leftrightarrow log(x_1) = log(x_2)$}, og det er i øvrigt baggrunden for, at man kan tage logaritmen på begge sider af lighedstegnet, når man løser ligninger (som her).

Logaritmisk vækst

Logaritmefunktioner har den egenskab, at en bestemt relativ ændring af x-værdien (et bestemt forhold mellem to x-værdier) giver en bestemt absolut ændring af y-værdien (husk at det omvendte gælder for eksponentialfunktioner, der jo som nævnt er omvendte funktioner til logaritmefunktionerne). For titalslogaritmen gælder fx, at en tidobling af x-værdien giver en øgning af y-værdien med 1. Hvis vi starter med x-værdien 1, som har y-værdien log(1)=0 fås således

x	1	10	100	1000	10000
log(x)	0	1	2	3	4

Hvis vi i stedet starter med x=5, som har y-værdien log(5)=0,69897, fås

x	5	50	500	5000	50000
log(x)	0,69897	1,69897	2,69897	3,69897	4,69897

Hvis vi igen starter med x-værdien x=1 og log(1)=0 men nu hele tiden fordobler x-værdien fås (y-værdien øges med 0,30103)

x	1	2	4	8	16
log(x)	0	0,30103	0,60206	0,90309	1,20412

Regneregler

Det er nyttigt at kunne følgende regneregler:

Regneregler for logaritmer: {$$ log(a\cdot b)=log(a)+log(b) $$} {$$ log(\frac{a}{b})=log(a)-log(b) $$} {$$ log(a^x)=x\cdot log(a) $$} De samme regneregler gælder også for alle andre logaritmefunktioner, herunder den naturlige logaritme

Læg mærke til, at den ovennævnte egenskab - at en bestemt relativ ændring af x-værdien giver en bestemt absolut ændring af y-værdien - følger af den første regneregel. Det ses nemlig, at når a ganges med et bestemt tal b , så øges y-værdien log(a) med det bestemte tal log(b).

Den sidste regneregel bruges fx til at løse ligninger af typen a^x = c. Det kan nemlig gøres sådan:

{$$ a^x=c $$}

{$$ log(a^x)=log(c) $$}

{$$ x\cdot log(a)=log(c) $$}

{$$x= \frac{log(c)}{log(a)} $$}

Sammenhæng mellem ln og log

Der er følgende sammenhæng mellem de to logaritmefunktioner: {$$ln(x) = \frac{log(x)}{log(e)} \qquad og \qquad log(x) = \frac{ln(x)}{ln(10)}$$}

Logaritmisk akse

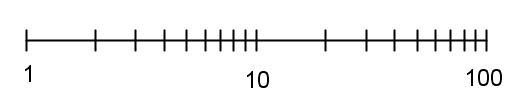
En logaritmisk akse er en akse, som er indrettet på den måde, at et bestemt stykke på aksen (fx en cm) svarer til en bestemt relativ ændring af værdierne på aksen (fx en fordobling). Der vil altså være samme afstand mellem værdierne 1 og 2 (en fordobling), 2 og 4, 4 og 8, 8 og 16 osv. Det kan ses på den logaritmiske akse på figuren herunder. Det ses også let, at en tidobling (fra 1 til 10 eller fra 10 til 100) svarer til det samme stykke på aksen. Det er altså forholdet mellem to tal, der bestemmer afstanden mellem dem på den logaritmiske akse, mens det på en almindelig (ækvidistant) akse er forskellen på to tal, der bestemmer deres indbyrdes afstand.

Logaritmiske akser bruges på såkaldt logaritmepapir. Der findes to slags, nemlig enkeltlogaritmisk papir, hvor y-aksen er logaritmisk, mens x-aksen er normal (ækvidistant), og dobbeltlogaritmisk papir, hvor både x-aksen og y-aksen er logaritmiske. Enkeltlogaritmisk papir har den egenskab, at grafer for eksponentielle funktioner bliver rette linjer herpå, mens potensfunktioners grafer bliver rette linjer på dobbeltlogaritmisk papir. Man kan således afgøre, om et givet datasæt bedst kan beskrives med en eksponentiel funktion eller en potensfunktion, ved at afsætte datasættets punkter på de to typer papir og se om de tilnærmelsesvis ligger på en ret linje. I praksis gøres det lettest i fx Excel, hvor akserne med et par klik kan gøres logaritmiske.

---