Kvadratrod 2 er et irrationalt tal
Det følgende bevis for, at {$\sqrt{2}$} er et irrationalt tal, er efter Euklid og er altså omkring 2300 år gammelt.
Der er tale om et såkaldt modstridsbevis. Denne bevistype fungerer på den måde, at man starter med en antagelse, som man derefter påviser fører til en modstrid, altså til en påstand som ikke er sand. Heraf kan man så konkludere, at antagelsen var usand.
Bevis
- Vi antager, at {$\sqrt{2}$} er et rationalt tal, hvilket betyder, at vi kan skrive {$\displaystyle\sqrt{2} = \frac{a}{b}$}. Vi kan endvidere antage, at brøken {$\displaystyle\frac{a}{b}$} er uforkortelig (enhver brøk kan jo forkortes indtil den er uforkortelig)
- Vi kvadrerer nu og får {$\displaystyle \Big(\frac{a}{b} \Big)^2 = 2$}, som også kan skrives {$\displaystyle\frac{a^2}{b^2} = 2$}
- Heraf følger at {$a^2 = 2b^2$}
- Men det betyder, at {$a^2$} er et lige tal
- Og så er a også et lige tal (Hvis man kvadrerer et ulige tal fås altid et ulige tal)
- Vi kan derfor skrive {$a=2k$}
- Dette indsættes i ligningen i 3): {$(2k)^2 = 2b^2$}, hvilket også kan skrives {$4k^2 = 2b^2$} eller {$2k^2 = b^2$}
- Men så er {$b^2$} og dermed {$b$} også et lige tal.
- Både a og b er således lige tal, og derfor er brøken {$\displaystyle \frac{a}{b}$} ikke uforkortelig (den vil jo kunne forkortes med 2).
- Dermed er vi nået frem til en modstrid, og derfor må den oprindelige antagelse om, at {$\sqrt{2}$} er et rationalt tal være falsk
- Ergo er {$\sqrt{2}$} et irrationalt tal
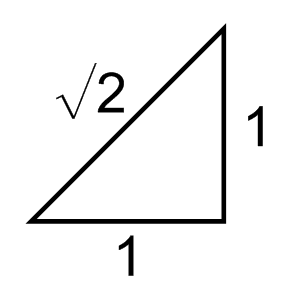
Geometrisk kan man tænke på {$\sqrt{2}$} som diagonalen i et kvadrat med sidelængden 1 eller som hypotenusen i en retvinklet trekant, hvor begge kateter har længden 1 (følger af Pythagoras' sætning - se figur).
Det, at {$\sqrt{2}$} er irrationalt, betyder så, at der ikke findes nogen måleenhed, som kan bruges til at angive længden af både kateterne og hypotenusen. Kateterne kan naturligvis måles med et utal af forskellige måleenheder. Fx kunne vi vælge måleenheden {$\displaystyle \frac{1}{1000000}$} (en milliontedel), og kateternes længde kan så angives som en million milliontedele ({$\displaystyle \frac{1000000}{1000000} = 1$}). Med da {$\sqrt{2}$} er irrational og altså slet ikke kan skrives som en brøk, kan man ikke angive længden af hypotenusen i milliontedele eller i nogen som helst anden måleenhed.
Pythagoræerne opdagede efter sigende dette fænomen, og da deres verdensbillede i høj grad var baseret på matematik og tal - og på det tidspunkt kendte man kun hele tal og brøker med hele tal i tæller og nævner - blev de naturligvis rystede i deres grundvold. Så rystede at de forsøgte at holde opdagelsen hemmelig, hvilket selvfølgelig var dømt til at mislykkes.